You're reading for free via Sai Viswanth's Friend Link. Become a member to access the best of Medium.
Would You Use ANOVA for Feature Selection?
Know A-Z of ANOVA with an interesting dataset.
We often forget the most crucial step when developing a Machine learning model — Feature Selection. Not selecting the right features correlated to the target variable can prevent your model from reaching the potential performance.
Feature Selection impacts the entire pipeline in two ways:-
- Removes useless and redundant features
- High probability of increasing the performance in the worst case no change in accuracy.
Choosing the right technique can help you to converge to the right set of features faster. Sometimes, you do have to find out by iteratively trying out various methods.
Filter methods rely on statistical formulations for ranking of the features on the other hand, wrapper methods use models to choose the appropriate features. In this article, we will focus on ANOVA — a filter method used for selecting the highly correlated features to our target variable
I want you to take a lot from this article, in the next few minutes, we are going to go through the following topics:-
- Clear Understanding of What is ANNOVA.
- How can you use ANOVA to implement on a dataset
- Powerful Visualizations
ANOVA
Analysis of Variance aka ANOVA is a statistical approach in helping us to understand the impact of a categorical feature on a target variable. It is an extension of a T-test, where a T-test is limited in testing for 2 groups, whereas ANOVA is for more than 2 groups present in a feature.

ANOVA hypothesis (First Step) :-
The hypothesis is like a preliminary conclusion based on limited evidence in hand so that we have a starting point for further investigation. Usually, two hypothesis statements are stated:-
H0 (Null Hypothesis) — No difference in the means of different groups.
H1 (Alternative Hypothesis) — At least there is one statistical difference between the means.
Statistical Proof
Strong evidence is required either to accept/reject the null hypothesis. An F-Test can help with it by providing us with a single value by taking the ratio between two variances.
F Value = Variance_1 / Variance_2
In ANOVA, the two variances are between-group variance(bgv) and Within-group variance(wgv). The between-group variance quantifies the distance between the groups and Within-group variance measures the spread of data points inside the group.

Between and Within Group Variance
The ANOVA can be represented in the form of the model equation which is similar to that of the Regression.

The slope in the Regression is meant to act as a model changing the slope means the model is finding patterns in the data to minimize the error, which is intercept c.
Similarly, the ANOVA model equation can be written as that of Generalized Eqn:-

The Model Sum of Squares(SSM) is between-group variance, whereas the Error Sum of Squares (SSE) is equated to within-group variance. The former signifies the model’s capability to predict an instance lying in a particular group, and the latter term is the uncertainty the model has.
Let's dive right in for the calculations:-
Model Sum of Squares
The distance between each group’s average value to the total average of all groups. This value has to be squared to negate the negative sum.

Error Sum of Squares
Summing up the distance from each data point in a group to its average and squaring it up, will give us the amount of dispersion in the group.

Until now, we have seen the theoretical concept of ANOVA. Without actually applying it on a dataset, it wouldn't be much fun.
Coffee Dataset - Let's Go !!!
To all the coffee lovers out there, we will use the ANOVA technique on a Kaggle Coffee dataset to see if the level of roasting on the coffee beans impacts the rating by consumers. Sounds interesting right, even though I don’t drink coffee 😅.What’s there in the Dataset
What’s there in the Dataset
A Coffee dataset does not have the type of seeds, which is Strange. Aside from that there are a total of 12 features, including origin, roast level, the type of roaster, and descriptions.

Roast and Ratings are the only features that will be taken for the ANOVA analysis. The roast feature has 5 unique classes — Medium-Light, Medium, Light, Medium-Dark, and Dark and Rating is a numerical feature that describes user satisfaction.

The roast feature is heavily poised with imbalanced data with very few instances in the dark class and 80% of the data lies in the Medium-Light. To balance it out:- we remove the underrepresented — Medium-Dark and Dark classes. Also, limit the Medium-Light class to 300 data points.

After doing the above steps for balancing, the boxplot of the three roast classes signifies that the distributions of the ratings are quite different. That being said one thing I noticed is the Median rating of Medium-Light is almost equal to the 75% percentile of the Medium-Roast Rating.
Define Hypothesis
Generally, this step is boring but necessary. We have to put forth the two hypothesis statements for our Coffee-dataset problem:-
Null Hypothesis:- Almost the same variance across the roast groups (i.e — Medium-Light, Medium, and Light)
Alternative Hypothesis:- At least one roast group variance is significant compared to the others.
Calculate SSM and SSE
I have written a simple Python code for the calculation, and the build of the code allowed me to break up my understanding into smaller components. In simple, we use these two values to help us figure out whether the variance of the groups is similar to that of the whole data distribution.
Model Sum of Squares
def calculate_ssm(data , n_groups):
# Empty array for means and datapoints
means = []
n = []
total_mean = 0
for i in data["roast"].unique():
group_mean = data[data["roast"]==i]["rating"].mean()
datapoints = data[data["roast"]==i]["rating"].shape[0]
# Caculate mean for each insurance provider and number of datapoints
means.append(group_mean)
n.append(datapoints)
# Total mean for all the groups
total_mean = np.mean(means)
# Difference between the individual group mean and the combined group mean
ssm_scores = []
for j in range(ngroups):
ssm_scores.append(n[j] * ((means[j] - total_mean) ** 2))
ssm = np.sum(ssm_scores)
return ssmYou can use this function to get the SSM value by inputting the data and number of groups. This function is not yet designed for any type of data, as in the code there are some hard-coded values.
Model Sum of Squares — 215.46
Error Sum of Squares
It is pretty simple code compared to the Model Sum of Squares:-
def calculate_sse(data):
sse = 0
for i , provider in enumerate(data["roast"].unique()):
for dp in data[data["roast"]==provider]["rating"].tolist():
sse += (dp - means[i]) ** 2
return sseBasically, it tells us the distribution of a group, like the ratings in the Medium-Light Roast group are far apart. It does the same thing for all the other groups — Medium and Light Roast. Suppose SSE is higher, then we can say that the groups don’t have a pattern; instead have more of like a random rating.
Error Sum of Squares — 2138.70
SSE is 10 times greater than SSM.
We will have to determine the Degrees of freedom(Df) for each value. Degrees of freedom are the number of variables you can vary to find the value of a dependent variable. In general, if you have N observations, then Df would be N-1. There are two Df to find:-
- Degrees of Freedom for Model SS = Number of Groups -- 1
- Degrees of Freedom for Error SS = Total No of Datapoints -- Number of Groups
In our coffee problem, we have 3 groups and no of datapoints -> 846
F - Value (Ratio)
We did all the preparations to arrive at this point. As we have discussed F-value is the ratio of two variances, with degrees of freedom into the frame let’s tweak the equation a bit:-
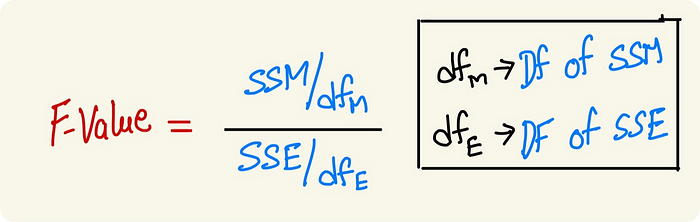
Degrees of freedom are at the denominator, making the Sum of Squares equivalent to a single instance in the sense that, SSM after dividing degrees of freedom, the value we get is for 1 group, similarly for SSE as well.
Substituting these values:-

Woah ! It seems like a huge value. With the alpha value set to 0.05 threshold (95% confidence), we will have to reject the null hypothesis if the P-value is less than 0.05 as there is no evidence.
The P-value is the probability of obtaining at least one significant observation. So using F-Value, we can calculate P-Value using a simple Python library — Stats

Our P-value for the Coffee roast data is almost near zero. It shows that the probability of having similar variances for our coffee roast data groups is near zero.
Relation to Feature Selection
In other terms, Medium-Light, Medium, and Light Roast Coffee have different distributions it is because a large number of people might have rated Medium or Light Roast higher or people didn’t like if their Coffee is on Medium-Light Roast.
The people's choices made a significant difference in the ratings, which proves that the roast type plays a huge role in predicting the ratings. With that said, this feature should be selected for training our machine learning model.
Conclusion
Hooray, cheer up, guys you have learned to use ANOVA. To apply it to your data, try out the sklearn f_classify function for ranking the features based on ANOVA analysis.
Let me know in the comments if it has worked on your dataset.
If you enjoyed reading this article please do follow me on medium for more updates. Help me reach 100 followers 😃😃😃.
References
These resources helped me to go deep for the ANOVA analysis








